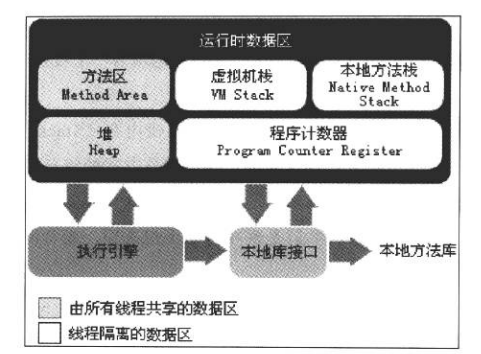
InnoDB表的限制 对InnoDB表的限制在本节中的以下主题下进行描述:
最大值和最小值
一个表最多可以包含1017列。虚拟生成的列包含在此限制中。
一个表最多可以包含64个辅助索引。
索引键前缀长度限制是使用DYNAMIC或COMPRESSED行格式的InnoDB表的3072字节。
索引键前缀长度限制是使用REDUNDANT或COMPACT行格式的InnoDB表的767字节。例如,在TEXT或VARCHAR列上,如果假设utf8mb4字符集和每个字符最多4个字节,则列前缀索引可能超过191个字符,从而达到此限制。